树形结构是算法中很常见的一种结构,正好工作中遇到了,就研究一下遍历、深度、查找节点等算法。
遍历
深度优先遍历的思想是从顶点开始,访问其第一个未被访问的邻节点,然后以该邻节点为顶点,重复以上步骤,直到所有节点被访问完。
广度优先遍历的思想是从顶点开始,访问其所有未被访问的邻节点,然后依次访问这些节点的子节点,直到所有节点被访问完。
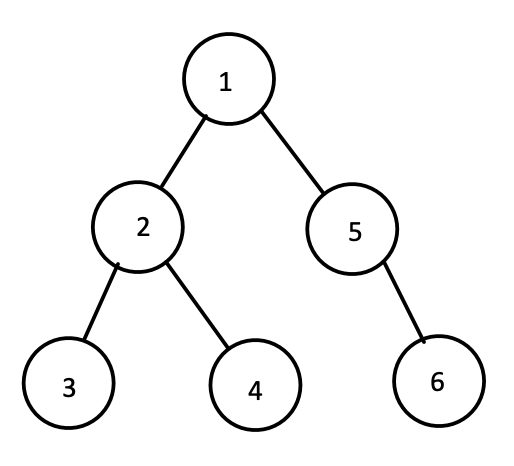
如上图,按深度优先遍历的顺序为1、2、3、4、5、6,按广度优先遍历的顺序为1、2、5、3、4、6。
有如下数组,将其展开为一维数组[1,2,3,4,5,6,7]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| let arr = [
[
1,
[
2,
3
]
],
[
4,
[
[
5,
6
],
7
]
]
];
|
深度优先
1
2
3
4
5
6
7
8
9
10
11
| function deepVisit(data, newData = []){
for(var i = 0; i < data.length; i++){
if(data[i] instanceof Array && data[i].length){
newData.concat(...deepVisit(data[i], newData))
}else{
newData.push(data[i])
}
}
return newData
}
deepVisit(arr)
|
广度优先
1
2
3
4
5
6
7
8
9
10
11
| function wideVisit(data){
let over = true
for(var i = 0; i < data.length; i++){
if(data[i] instanceof Array && data[i].length){
over = false
data.splice(i,1,...data[i])
}
}
return over ? data : ideVisit(data)
}
wideVisit(arr)
|
标记和查找
有如下结构,标记每个节点的深度、查找深度为n的所有节点、查找所有的叶子节点(末端节点)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| let arr = [
{
a:1,
children: [
{
a:2,
children: [
{
a:3
},
{
a:4
}
]
}
]
},
{
a:5,
children: [
{
a:6
}
]
}
];
|
数组的树结构如图所示

其中3、4、6为叶子节点。
下面对arr数组进行遍历,给每个节点编上号,并标示其层级。
标记深度和编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function mark(data, keyNode = 1, depth = 1){
for(var i = 0; i < data.length; i++){
data[i].keyNode = keyNode++
data[i].depth = depth
if(data[i].children && data[i].children.length){
let result = mark(data[i].children, keyNode, depth+1)
keyNode = result.keyNode
}
}
return {
keyNode: keyNode
}
}
mark(arr)
console.log(arr)
|
运行结果如下,arr的每个节点已经被编号用keyNode字段标示并用depth字段标示深度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| [
{
"a": 1,
"children": [
{
"a": 2,
"children": [
{
"a": 3,
"keyNode": 3,
"depth": 3
},
{
"a": 4,
"keyNode": 4,
"depth": 3
}
],
"keyNode": 2,
"depth": 2
}
],
"keyNode": 1,
"depth": 1
},
{
"a": 5,
"children": [
{
"a": 6,
"keyNode": 6,
"depth": 2
}
],
"keyNode": 5,
"depth": 1
}
]
|
查找叶子节点
1
2
3
4
5
6
7
8
9
10
11
12
| function findLeaf(data, leaf = []){
for(var i = 0; i < data.length; i++){
if(data[i].children && data[i].children.length){
let result = findLeaf(data[i].children, leaf)
leaf.concat(...leaf)
}else{
leaf.push(data[i])
}
}
return leaf
}
console.log(findLeaf(arr))
|
运行结果如下,即所有叶子节点的集合。
1
2
3
4
5
6
7
8
9
10
11
| [
{
"a": 3
},
{
"a": 4
},
{
"a": 6
}
]
|
查找keyNode为n的节点
1
2
3
4
5
6
7
8
9
10
11
12
13
| function findNode(data, keyNode){
for(var i = 0; i < data.length; i++){
if(data[i].keyNode === keyNode){
return data[i]
}
if(data[i].children && data[i].children.length){
return findNode(data[i].children, keyNode)
}
}
return {}
}
deepVisit(arr)
console.log(findNode(arr,4))
|
运行结果如下。
1
2
3
4
5
| {
"a": 4,
"keyNode": 4,
"depth": 3
}
|
查找深度为n的节点
1
2
3
4
5
6
7
8
9
10
11
| function findNode(data, depth, curDepth = 1, result = []){
for(var i = 0; i < data.length; i++){
if(curDepth === depth){
result.push(data[i])
}else if(data[i].children && data[i].children.length){
findNode(data[i].children, depth, curDepth+1, result)
}
}
return result
}
console.log(findNode(arr,2))
|
运行结果如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| [
{
"a": 2,
"children": [
{
"a": 3
},
{
"a": 4
}
]
},
{
"a": 6
}
]
|
以上均是运用递归思想,通过传参和返回值的形式保留每一步的运算结果,理解了作用域和函数的返回值,那遍历树结构就不复杂了。

